Zer dira palankak?
Palankak funtsezko tresnak dira fisikan, eta indarra eta mugimendua transmititzeko erabiltzen diren makina sinpleak dira. Hiru palanka mota nagusi daude: lehen klasea, bigarren klasea eta hirugarren klasea.
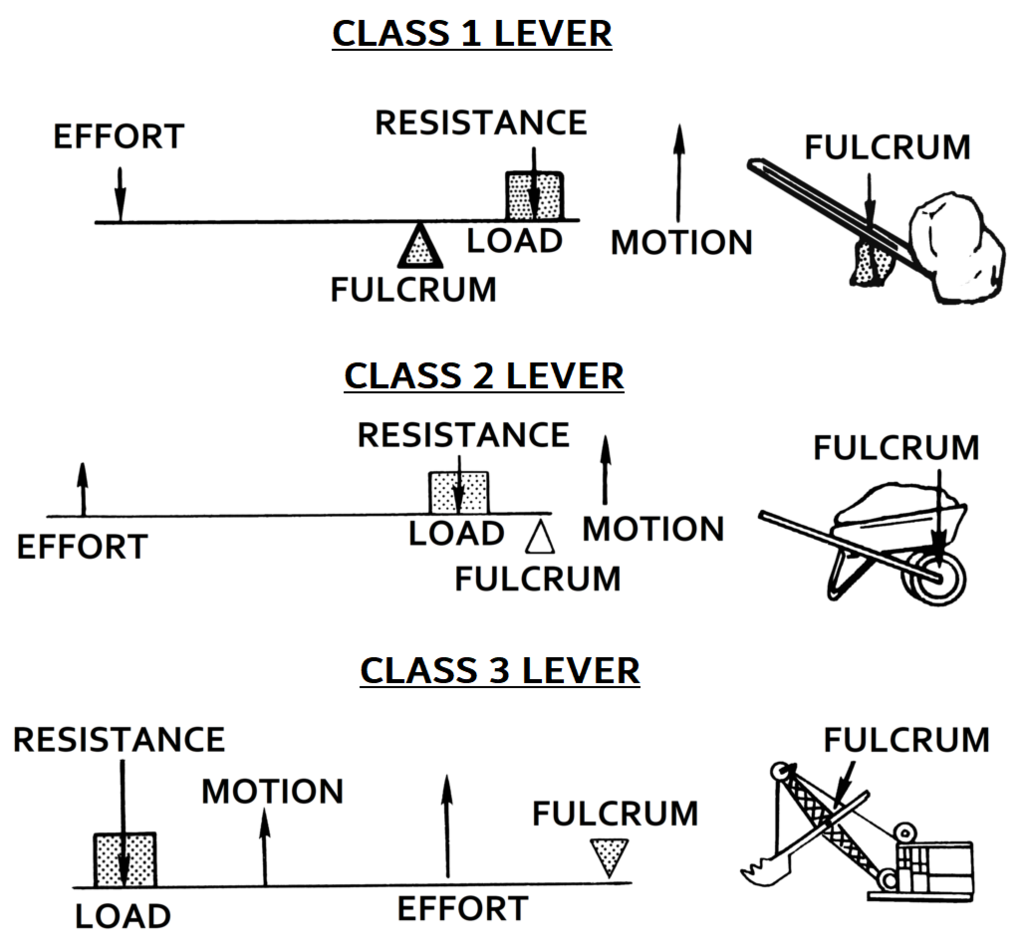
Lehen mailako palanka da euskarri-puntua, fulkroa ere esaten zaiona, indarraren aplikazio-puntuaren eta erresistentzia-puntuaren artean dagoena. Palanka mota honek aukera ematen du jatorrian aplikatutako indarra baino gehiago aplikatzeko, eta horrek objektu astunak altxatzea errazten du. Lehen mailako palankaren adibide komun bat palanka-barra bat da.
Bigarren mailako palanka da euskarri-puntua indarraren aplikazio-puntuaren eta erresistentzia-puntuaren artean dagoena. Palanka mota honek aukera ematen du jatorrian aplikatutako indarra baino indar handiagoa aplikatzeko, baina ahalegin handiagoa egin behar da objektua mugitzeko. Bigarren mailako palankaren adibide komun bat guraize bat da.
Hirugarren motako palanka da euskarri-puntua indarraren aplikazio-puntutik eta erresistentzia-puntutik kanpo dagoena. Palanka mota honek esfortzu handiagoa eskatzen du objektua mugitzeko, eta ez du aukerarik ematen jatorrian aplikatutako indarra baino indar handiagoa aplikatzeko. Hirugarren mailako palankaren adibide komun bat erratza da.
Kontuan izan behar da palanka baten eraginkortasuna palankaren besoen luzeraren eta indarra aplikatzeko puntutik eta erresistentzia-puntura dagoen distantziaren araberakoa dela. Zenbat eta laburragoa izan indarra aplikatzeko erabiltzen den besoa eta zenbat eta luzeagoa izan indarrari eusteko erabiltzen den besoa, orduan eta errazagoa izango da objektua mugitzea.
Laburbilduz, palankak indarra eta mugimendua transmititzeko tresna erabilgarriak dira, eta hiru palanka mota nagusi daude: lehen klasekoa, bigarren klasekoa eta hirugarren klasekoa. Palanka horietako bakoitzak bere ezaugarriak ditu, eta egoera desberdinetan erabiltzen dira, objektu bat mugitzeko behar den indarraren eta ahaleginaren arabera.
Palanka mota bakoitzaren ariketa bana
1. ariketa (lehen mailako palanka): Palanka-barra batek 2 metroko luzera du eta eskumako muturretik metro batera dagoen fulkro baten gainean bermatuta dago. Pertsona batek 50 N-ko indarra aplikatzen du barraren ezkerreko muturrean, eta 100 N-ko objektu bat altxatzen du eskuineko muturrean. Zer indar aplikatu behar du pertsonak barraren ezkerreko muturrean objektua altxatzeko?
Soluzioa: Lehen klaseko palankak aukera ematen du jatorrian aplikatutako indarra baino indar gehiago aplikatzeko. Barraren ezkerreko muturrean aplikatzen den indarrari aplikazio-indarra esaten zaio, eta barraren eskuineko muturrean dagoen indarrari, berriz, erresistentzia-indarra. Bi indar horien arteko erlazioa kalkulatzeko, lehen mailako palankaren formula erabil daiteke: F1/F2 = L1/L2, non F1 aplikazio-indarra den, F2 erresistentzia-indarra den, L1 aplikazio-besoaren luzera den eta L2 erresistentzia-besoaren luzera den.
Ariketa honetan, aplikazio-indarra F1 = 50 N da, erresistentzia-indarra F2 = 100 N, aplikazio-besoaren luzera L1 = 2 metro eta erresistentzia-besoaren luzera L2 = 1 metro. Formula erabiliz, objektua altxatzeko behar den aplikazio-indarra kalkula dezakegu:
F1 = (F2* L1)/L2
= (100 N* 2 m)/1 m
= 200 N
Beraz, pertsonak 200 N-ko indarra aplikatu behar du barraren ezkerreko muturrean, 100 N-ko objektua eskuineko muturrean altxatzeko.
2. ariketa (bigarren mailako palanka): artazi batek metro bateko luzera du guztira, eta eskumako muturretik 0,5 metrora dagoen fulkro baten gainean tenkatuta dago. Pertsona batek 50 N-ko indarra aplikatzen du guraizearen ezkerreko muturrean, eta 100 N-ko erresistentzia-objektu bat mozten du eskuineko muturrean. Zer indar aplikatu behar du pertsonak guraizearen ezkerreko muturrean objektua mozteko?
Soluzioa: Bigarren klaseko palankak aukera ematen du jatorrian aplikatutako indarra baino indar handiagoa aplikatzeko, baina ahalegin handiagoa egin behar da objektua mugitzeko. Ezkerreko muturrean aplikatzen den indarra artaziaren aplikazio-indarra bezala ezagutzen da, eta guraizearen eskuineko muturreko indarra erresistentzia-indarra bezala. Bi indar horien arteko erlazioa kalkulatzeko, bigarren mailako palankaren formula erabil daiteke: F1/F2 = L2/L1, non F1 aplikazio-indarra den, F2 erresistentzia-indarra den, L1 aplikazio-besoaren luzera den eta L2 erresistentzia-besoaren luzera den.
Ariketa honetan, aplikazio-indarra F1 = 50 N da, erresistentzia-indarra F2 = 100 N, aplikazio-besoaren luzera L1 = 0,5 metro eta erresistentzia-besoaren luzera L2 = 0,5 metro. Formula erabiliz, objektua mozteko beharrezkoa den aplikazio-indarra kalkula dezakegu:
F1 = (F2* L2)/L1
= (100 N* 0,5 m)/0,5 m
= 100 N
Beraz, pertsonak 100 N-ko indarra aplikatu behar du guraizearen ezkerreko muturrean, eskuineko muturrean 100 N-ko objektua mozteko.
3. ariketa (hirugarren mailako palanka): Erratz batek 1,5 metroko luzera du guztira, eta eskumako muturretik 0,5 metrora dagoen fulkro baten gainean tenkatuta dago. Pertsona batek 50 N-ko indarra aplikatzen du erratzaren ezkerreko muturrean, eta 100 N-ko erresistentzia-objektu bat erratzen du eskuineko muturrean. Zer indar aplikatu behar du pertsonak erratzaren ezkerreko muturrean objektua errazteko?
Soluzioa: Hirugarren klaseko palankak esfortzu handiagoa eskatzen du objektua mugitzeko eta ez du aukerarik ematen jatorrian aplikatutako indarra baino gehiago aplikatzeko. Erratzaren ezkerreko muturrean aplikatzen den indarrari aplikazio-indarra esaten zaio, eta erratzaren eskuineko muturrean dagoen indarrari erresistentzia-indarra. Bi indar horien arteko erlazioa kalkulatzeko, hirugarren motako palankaren formula erabil daiteke: F1/F2 = L1/L2, non F1 aplikazio-indarra den, F2 erresistentzia-indarra den, L1 aplikazio-besoaren luzera den eta L2 erresistentzia-besoaren luzera den.
Ariketa honetan, aplikazio-indarra F1 = 50N da. Erresistentzia-indarra F2 = 100 N da, aplikatzeko besoaren luzera L1 = 1,5 metro da eta erresistentzia-besoaren luzera L2 = 0,5 metro. Formula erabiliz, objektua erraztatzeko beharrezkoa den aplikazio-indarra kalkula dezakegu:
F1 = (F2* L1)/L2
= (100 N* 1,5 m)/0,5 m
= 300 N
Beraz, pertsonak 300 N-ko indarra aplikatu behar du erratzaren ezkerreko muturrean, eskuineko muturrean 100 N-ko objektua erratza kentzeko.
Garrantzitsua da kontuan hartzea adibide horiek argigarriak baino ez direla eta bizitza errealean objektu bat mugitzeko behar den indarra aldatu egin daitekeela, objektuaren marruskadura eta erresistentzia bezalako faktoreen ondorioz. Gainera, garrantzitsua da kontuz ibiltzea palankak erabiltzean eta segurtasun-jarraibide egokiak betetzea lesioak edo kalteak saihesteko.
*Adimen artifizialarekin osatutako sarrera
